Monkey patched classes

These are functionalities added to other libraries, or “monkey-patched” them. How is this possible? Check out k1lib.patch().

k1lib._monkey.dummy()

Does nothing. Only here so that you can read source code of this file and see what’s up.

Class torch.nn.Module

Module.getParamsVector() → List[torch.Tensor]

For each parameter, returns a normal distributed random tensor with the same standard deviation as the original parameter

Module.importParams(params: List[torch.nn.parameter.Parameter])

Given a list of torch.nn.parameter.Parameter/torch.Tensor, update the current torch.nn.Module’s parameters with it’

Module.exportParams() → List[torch.Tensor]

Gets the list of torch.Tensor data

Module.paramsContext()

A nice context manager for importParams() and exportParams(). Returns the old parameters on enter context. Example:

m = nn.Linear(2, 3)
with m.paramsContext() as oldParam:
    pass # go wild, train, mutate `m` however much you like
# m automatically snaps back to the old param

Small reminder that this is not foolproof, as there are some Module that stores extra information not accessible from the model itself, like BatchNorm2d.

Module.deviceContext(buffers: bool = True) → AbstractContextManager

Preserves the device of whatever operation is inside this. Example:

import torch.nn as nn
m = nn.Linear(3, 4)
with m.deviceContext():
    m.cuda() # moves whole model to cuda
# automatically moves model to cpu

This is capable of preserving buffers’ devices too. But it might be unstable. Parameter are often updated inline, and they keep their old identity, which makes it easy to keep track of which device the parameters are on. However, buffers are rarely updated inline, so their identities change all the time. To deal with this, this does something like this:

devices = [buf.device for buf in self.buffers()]
yield # entering context manager
for buffer, device in zip(self.buffers(), devices):
    buffer.data = buffer.data.to(device=device)

This means that while inside the context, if you add a buffer anywhere to the network, buffer-device alignment will be shifted and wrong. So, register all your buffers (aka Tensors attached to Module) outside this context to avoid headaches, or set buffers option to False.

If you don’t know what I’m talking about, don’t worry and just leave as default.

Parameters

buffers – whether to preserve device of buffers (regular Tensors attached to Module) or not.

Module.gradContext()

Preserves the requires_grad attribute. Example:

m = nn.Linear(2, 3)
with m.gradContext():
    m.weight.requires_grad = False
# returns True
m.weight.requires_grad

It’s worth mentioning that this does not work with buffers (Tensors attached to torch.nn.Module), as buffers are not meant to track gradients!

Module.__ror__(x)

Allows piping input to torch.nn.Module, to match same style as the module k1lib.cli. Example:

# returns torch.Size([5, 3])
torch.randn(5, 2) | nn.Linear(2, 3) | cli.shape()

Module.select(css: str = '*') → k1lib.selector.ModuleSelector

Creates a new ModuleSelector, in sync with a model. Example:

mS = selector.select(nn.Linear(3, 4), "#root:propA")

Or, you can do it the more direct way:

mS = nn.Linear(3, 4).select("#root:propA")

Parameters

• model – the torch.nn.Module object to select from

• css – the css selectors

Module.nParams

Get the number of parameters of this module. Example:

# returns 9, because 6 (2*3) for weight, and 3 for bias
nn.Linear(2, 3).nParams

Class torch.Tensor

Tensor.crissCross() → torch.Tensor

Concats multiple 1d tensors, sorts it, and get evenly-spaced values. Also available as torch.crissCross() and crissCross(). Example:

a = torch.tensor([2, 2, 3, 6])
b = torch.tensor([4, 8, 10, 12, 18, 20, 30, 35])

# returns tensor([2, 3, 6, 10, 18, 30])
a.crissCross(b)

# returns tensor([ 2,  4,  8, 10, 18, 20, 30, 35])
a.crissCross(*([b]*10)) # 1 "a" and 10 "b"s

# returns tensor([ 2,  2,  3,  6, 18])
b.crissCross(*([a]*10)) # 1 "b" and 10 "a"s

Note how in the second case, the length is the same as tensor b, and the contents are pretty close to b. In the third case, it’s the opposite. Length is almost the same as tensor a, and the contents are also pretty close to a.

Tensor.histBounds(bins=100) → torch.Tensor

Flattens and sorts the tensor, then get value of tensor at regular linspace intervals. Does not guarantee bounds’ uniqueness. Example:

# Tensor with lots of 2s and 5s
a = torch.Tensor([2]*5 + [3]*3 + [4] + [5]*4)
# returns torch.tensor([2., 3., 5.])
a.histBounds(3).unique()

The example result essentially shows 3 bins: \([2, 3)\), \([3, 5)\) and \([5, \infty)\). This might be useful in scaling pixels so that networks handle it nicely. Rough idea taken from fastai.medical.imaging.

Tensor.histScaled(bins=100, bounds=None) → torch.Tensor

Scale tensor’s values so that the values are roughly spreaded out in range \([0, 1]\) to ease neural networks’ pain. Rough idea taken from fastai.medical.imaging. Example:

# normal-distributed values
a = torch.randn(1000)
# plot #1 shows a normal distribution
plt.hist(a.numpy(), bins=30); plt.show()
# plot #2 shows almost-uniform distribution
plt.hist(a.histScaled().numpy()); plt.show()

Plot #1:

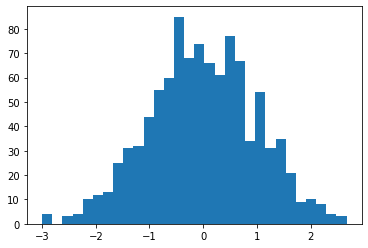
Plot #2:

Parameters

• bins – if bounds not specified, then will scale according to a hist with this many bins

• bounds – if specified, then bins is ignored and will scale according to this. Expected this to be a sorted tensor going from min(self) to max(self).

Tensor.clearNan(value: float = 0.0) → torch.Tensor

Sets all nan values to a specified value. Example:

a = torch.randn(3, 3) * float("nan")
a.clearNan() # now full of zeros

Tensor.hasNan() → bool

Returns whether this Tensor has any nan values at all.

Tensor.hasInfs()

Whether this Tensor has negative or positive infinities.

Module torch

torch.loglinspace(b, n=100, **kwargs)

Like torch.linspace(), but spread the values out in log space, instead of linear space. Different from torch.logspace()

Class graphviz.dot.Digraph

Digraph.__call__(_from, *tos, **kwargs)

Convenience method to quickly construct graphs. Example:

g = k1lib.graph()
g("a", "b", "c")
g # displays arrows from "a" to "b" and "a" to "c"

Class graphviz.dot.Graph

Graph.__call__(_from, *tos, **kwargs)

Convenience method to quickly construct graphs. Example:

g = k1lib.graph()
g("a", "b", "c")
g # displays arrows from "a" to "b" and "a" to "c"

Class mpl_toolkits.mplot3d.axes3d.Axes3D

Axes3D.march(heatMap, level: float = 0, facecolor=[0.45, 0.45, 0.75], edgecolor=None)

Use marching cubes to plot surface of a 3d heat map. Example:

plt.k3d(6).march(k1lib.perlin3d(), 0.17)

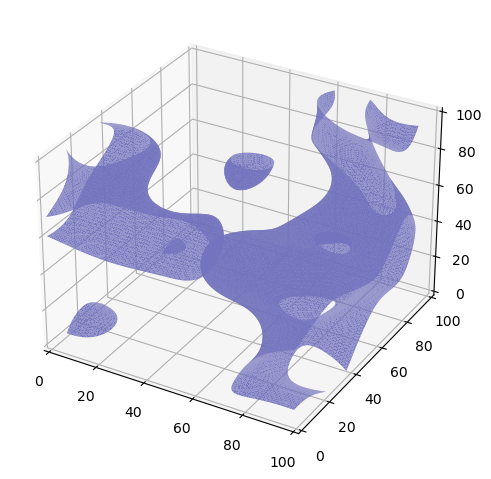
A more tangible example:

t = torch.zeros(100, 100, 100)
t[20:30,20:30,20:30] = 1
t[80:90,20:30,40:50] = 1
plt.k3d().march(t.numpy())

The function name is “march” because how it works internally is by using something called marching cubes.

Parameters

• heatMap – 3d numpy array

• level – array value to form the surface on

Axes3D.surface(z, **kwargs)

Plots 2d surface in 3d. Pretty much exactly the same as plot_surface(), but fields x and y are filled in automatically. Example:

x, y = np.meshgrid(np.linspace(-2, 2), np.linspace(-2, 2))
plt.k3d(6).surface(x**3 + y**3)

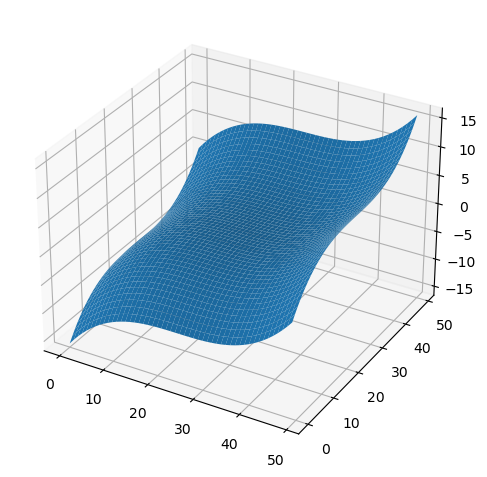
Parameters

• z – 2d numpy array for the heights

• kwargs – keyword arguments passed to plot_surface

Axes3D.plane(origin, v1, v2=None, s1: float = 1, s2: float = 1, **kwargs)

Plots a 3d plane.

Parameters

• origin – origin vector, shape (3,)

• v1 – 1st vector, shape (3,)

• v2 – optional 2nd vector, shape(3,). If specified, plots a plane created by 2 vectors. If not, plots a plane perpendicular to the 1st vector

• s1 – optional, how much to scale 1st vector by

• s2 – optional, how much to scale 2nd vector by

• kwargs – keyword arguments passed to plot_surface()

Axes3D.point(v, **kwargs)

Plots a 3d point.

Parameters

• v – point location, shape (3,)

• kwargs – keyword argument passed to scatter()

Axes3D.line(v1, v2, **kwargs)

Plots a 3d line.

Parameters

• v1 – 1st point location, shape (3,)

• v2 – 2nd point location, shape (3,)

• kwargs – keyword argument passed to plot()

Module matplotlib.pyplot

pyplot.k3d(size=8)

Convenience function to get an Axes3D.

Parameters

• labels – whether to include xyz labels or not

• size – figure size